Teorema de LAPLACE
O determinante de uma matriz quadrada de ordem 2 é igual à soma dos produtos dos elementos de uma fila qualquer pelos respectivos co-fatores.
Aplicação
Calcule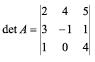
Procedimentos
I. Escolhe-se uma fila qualquer do determinante: 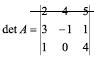
II. Coloca-se o sinal correspondente à potência (-1)i+j, do cálculo do co-fator, em cima dos elementos da fila selecionada: 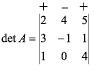
III. Multiplica-se cada elemento da fila selecionada, com o sinal do co-fator, pelo seu menor complementar.
det A = a11A11 + a12A12 + a13A13
Regra de CHIÓ
Para calcular o determinante de uma matriz de ordem n > 3 é necessário abaixar a ordem. Uma das maneiras é usar o Teorema de Laplace. Existe, além disso, uma regra prática dada por Chió que consiste em:
1.º Escolher um elemento aij = 1 (caso não exista, aplicar as propriedades para que apareça o elemento 1).
2.º Suprimir a linha (i) e a coluna (j) do elemento aij = 1, obtendo-se o menor complementar do referido elemento.
3.º Subtrair de cada elemento do menor complementar obtido o produto dos elementos que ficam nos pés das perpendiculares traçadas do elemento considerado às filas suprimidas.
4.º Multiplicar o determinante obtido no 3.º item por (-1)i+j onde i e j designam as ordens da linha e da coluna às quais pertence o elemento aij = 1.
Exemplo: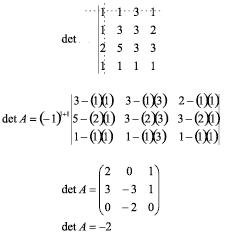
É papel do educador combater o medo de errar que inibe, as possibilidades de realização e satisfação. "Prof. Marcondes Diniz Martins"
terça-feira, 12 de maio de 2009
Teorema de LAPLACE
Produto de Matrizes
Se é um número real, o produto desse número por uma matriz A = (aij)mxn é uma matriz B = (bij)mxn tal que bij =
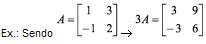
Propriedades do Produto de um Número por uma Matriz
Se A e B são matrizes de mesma ordem e e são números reais, valem as seguintes propriedades:
a) 1A = A
b)
c)
d) (
e) (
Produto de Matrizes
Dadas duas matrizes A = (aij)mxn e B = (bij)mxn, o produto da matriz A pela matriz B, nesta ordem, somente será possível quando o número de colunas da matriz A for igual ao número de linhas da matriz B.
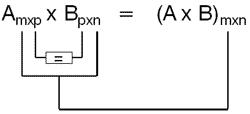
A matriz produto (A x B)mxn terá número de linhas de A e número de colunas de B.
Os elementos da matriz produto são obtidos multiplicando-se cada elemento das linhas da matriz A pelo correspondente elemento das colunas da matriz B e adicionando os produtos obtidos.
Propriedades do Produto de Matrizes
Sendo A, B, C matrizes, e a um número real, e supondo as operações abaixo possíveis, temos que:
a) A.(B.C) = (A.B).C (ASSOCIATIVA)
b) A.(B+C) = A.B + A.C (DISTRIBUTIVA À DIREITA)
c) (A+B).C = A.C+B.C (DISTRIBUTIVA À ESQUERDA)
d)
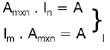 I É A IDENTIDADE
I É A IDENTIDADEe) (A . B) = A . (B) = . (A . B)
f) (A . B)T = BT . AT
Observações Importantes:
1.ª A multiplicação de matrizes não é comutativa, isto é, existem matrizes A e B tais que AB
2.ª Na multiplicação de matrizes não vale o anulamento do produto, isto é, podemos ter A . B = 0 mesmo com A
3.ª Não vale também a simplificação, isto é, podemos ter AB = AC, mesmo com A
Matriz Inversa
Uma matriz quadrada A de ordem n diz-se inversível ou não singular se, e somente se, existir uma matriz que indicamos por A-1, denominada inversa de A, tal que:
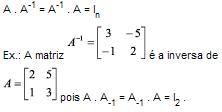
Operações com Matrizes
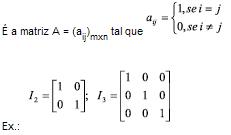
Matriz Transposta (At)
É a matriz que se obtém trocando ordenadamente as linhas pelas colunas da matriz dada.
Se B = (bij)mxn é transposta de A = (aij)mxn, então bij = aij.
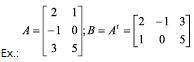
Matriz Diagonal
É uma matriz quadrada onde aij = 0, para i
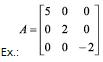
Matriz Simétrica
É uma matriz quadrada A tal que At = A, isto é, aij = aij para i j.
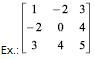
Matriz Anti-simétrica
É uma matriz quadrada A tal que At = -A , isto é, aij = -aij para i e j quaisquer.
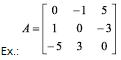
Operações com Matrizes
Igualdade de Matrizes
Duas matrizes A = (aij)mxn e B = (bij)mxn de mesma ordem, são iguais se, e somente se, aij = bij.
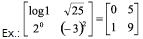
Propriedades da Igualdade
- Se A = B, então At = Bt
- (At)t = A
Adição e subtração de Matrizes
A soma de duas matrizes A = (aij)mxn e B = (bij)mxn de mesma ordem é uma matriz C = (aij)mxn tal que C = aij + bij.
A subtração de matrizes é dada pela sentença:
A – B = A + (– B )
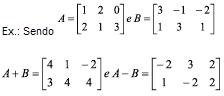
Propriedades da adição de Matrizes
a) A + B = B + A (COMUTATIVA)
b) (A + B) + C = A + (B + C) (ASSOCIATIVA)
c) A + 0 = 0 + A = A (ELEMENTO NEUTRO)
d) A + (-A) = (-A) + A = 0 (ELEMENTO OPOSTO)
e) (A + B)T = AT + BT (TRANSPOSTA DA SOMA)
Fórmula do Termo Geral
Fórmula do Termo Geral
CLASSIFICAÇÃO
Quanto à razão, as progressões aritméticas podem ser classificadas em:
1. Crescentes – São aquelas cuja razão é positiva.
Exemplo:
(4, 8, 12...) →r = 4 > 0 (positiva)
2. Decrescentes – São aquelas cuja razão é negativa.
Exemplo:
(10, 7, 4, 1, –2, –5)→ r = – 3 < 0 (negativa)
3. Constantes – São aquelas cuja razão é nula.
Exemplo:
(6, 6, 6, 6) →r = 0
FÓRMULA DO TERMO GERAL
Para obter o enésimo termo de uma P.A., basta somar (n – 1) vezes a razão ao primeiro termo. Com isso, podemos achar qualquer termo dentro de uma PA pela expressão:
an = a1 + (n - 1) . r
Em que:
an é o enésimo termo (termo geral);
a1 é o primeiro termo;
n é o número de termos;
r é a razão.
Aplicação
Qual é o quinto termo da P. A. (3, 6...)?
Solução:
a1 = 3
r = 6 – 3 = 3
n = 5
an = a1 + (n - 1) . r
a20 = 3 + (5 – 1). 3
a20 = 3 + 4.3
a20 = 15
INTERPOLAÇÃO ARITMÉTICA
Interpolar ou inserir k meios aritméticos entre dois termos extremos a e b de uma progressão aritmética significa obter uma P. A. com (k + 2) termos.
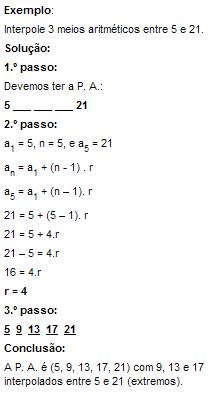
Equações exponenciais
Equações exponenciais
Uma equação é chamada exponencial quando a incógnita a ser determinada comparece como expoente.
Para resolver uma equação exponencial, você deve reduzir ambos os membros da igualdade a uma mesma base. Então, basta igualar os expoentes para recair numa equação comum.
Há equações exponenciais em que não é possível reduzir de imediato os dois membros à mesma base. Para resolvê-las, freqüentemente é conveniente utilizar uma variável auxiliar.
Aplicações
01. Resolva a equação 5x = 125.
Solução:
5x = 125→ 5x = 5 3 →x = 3
02. Resolva a equação 32x + 4.3x + 3 = 0.
Solução:
A expressão dada pode ser escrita na forma:
(3x)2 - 4.3x + 3 = 0
Fazendo 3x = y, temos:
y2 – 4y + 3 = 0 y = 1 ou y = 3
Como 3x= y, então 3x= 1 x = 0 ou 3x = 3 x = 1
Portanto, S = {0,1}.
Inequações exponenciais
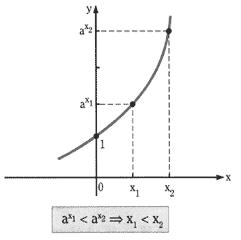
Dada uma desigualdade de potências, sendo an > am:
1.º caso – Se a > 1, então n > m (se as bases de duas potências são iguais e maiores que 1, é maior a potência de maior expoente, ou seja, a desigualdade é conservada)
1.° caso: a > 1