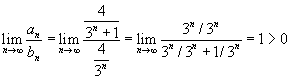CONVERGÊNCIA ABSOLUTA
Definição: Uma série ![]() é absolutamente convergente se a série dos módulos
é absolutamente convergente se a série dos módulos
![]() é convergente.
é convergente.
Ex: A série alternada ![]() é absolutamente convergente, pois a série dos módulos
é absolutamente convergente, pois a série dos módulos ![]() é uma série-p, com p=2 > 1 e, portanto, convergente.
é uma série-p, com p=2 > 1 e, portanto, convergente.
TEOREMA
Se uma série infinita ![]() é absolutamente convergente, então a série é convergente.
é absolutamente convergente, então a série é convergente.
TESTE DE D'ALEMBERT
Seja ![]() uma série de termos não nulos e seja
uma série de termos não nulos e seja 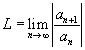 . Então:
. Então:
* Se L <> ABSOLUTAMENTE CONVERGENTE.
* Se L > 1, (incluindo L = 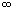 ), a série é DIVERGENTE.
), a série é DIVERGENTE.
* Se L = 1, o teste falha (nada se pode afirmar).
RESUMO
TESTE | SÉRIE | CONVERGÊNCIA ou DIVERGÊNCIA | COMENTÁRIOS |
| da DIVERGÊNCIA ou do N-ÉSIMO TERMO | DIVERGE se | Nada se pode afirmar se | |
| SÉRIE GEOMÉTRICA | * CONVERGE e tem soma | Útil para testes de comparação | |
| SÉRIE-P | * CONVERGE se p > 1 * DIVERGE se p | Útil para testes de comparação | |
| da COMPARAÇÃO no limite | an > 0, bn > 0 | * Se * Se * Se | A série de comparação Para achar bn, consideram-se apenas os termos de an que têm maior efeito. |
| de LEIBNIZ | ALTERNADA
an > 0 | CONVERGE se: * * A série | Aplicável somente a séries alternadas. Se o primeiro item é falso, aplica-se o TESTE DA DIVERGÊNCIA. |
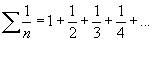 é chamada SÉRIE HARMÔNICA e, de acordo com o teorema, é divergente.
é chamada SÉRIE HARMÔNICA e, de acordo com o teorema, é divergente. 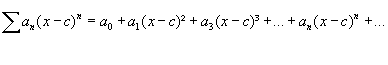
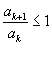 .
.