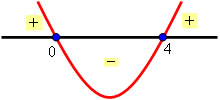
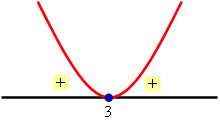
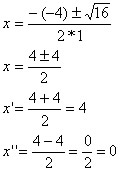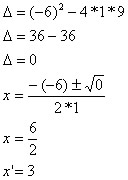ax2 + bx + c = 0
Dessa forma geral, podemos encontrar duas raízes reais x’ e x”, utilizando Bháskara.
SOMA
Somando as duas raízes:
x’ + x”
- b - √∆ - b + √∆ → +√∆ e -√∆ cancelam, pois sua soma será zero.
2a
-2b :2
2a :2
-b
a
Portanto, somar as duas raízes de uma equação do segundo grau é o mesmo que:
x’ + x” = -b
a
Multiplicando as duas raízes:
x’ . x”
x’ . x” = c
a
Além de utilizarmos a fórmula de Bháskara para encontrarmos o valor de x’ e x”, podemos utilizar o produto e a soma das raízes, veja como:
Dada a equação x2 – 7x + 10 = 0. Para encontrar a soma e o produto de suas raízes não é necessário que saibamos qual é o valor delas, mas devemos retirar da equação os seus coeficientes.
a = 1
b = - 7
c = 10
Chegamos a duas conclusões: a soma dessas raízes será 7 e o produto delas será 10. Por tentativas podemos encontrar números que multiplicados resultem em 10.
5 . 2 = 10
(-5) . (-2) = 10
1 . 10 = 10
(-1) . (-10) = 10
Desses produtos deve-se escolher aquele que se somarmos os seus fatores encontraremos como resultado 7.
5 + 2 = 7
Portanto, x’ = 5 e x” = 2.